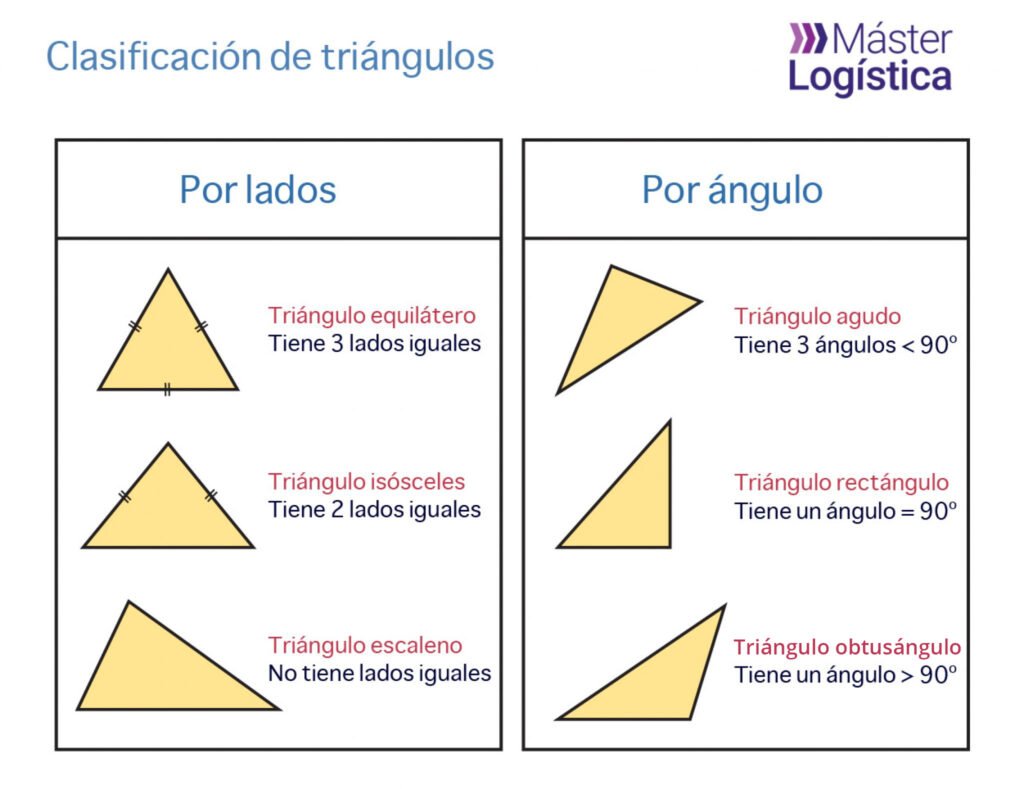
✅ Existen triángulos acutángulos (todos los ángulos menores de 90°), rectángulos (un ángulo de 90°) y obtusángulos (un ángulo mayor de 90°).
Los triángulos se pueden clasificar según sus ángulos en tres tipos principales: triángulos agudos, triángulos rectángulos y triángulos obtusos. Cada uno de estos tipos tiene características particulares que los diferencian entre sí. Un triángulo agudo posee todos sus ángulos menores de 90 grados, el triángulo rectángulo tiene un ángulo exactamente de 90 grados, y el triángulo obtuso cuenta con un ángulo mayor de 90 grados.
Para entender mejor estas clasificaciones, es útil considerar las propiedades y aplicaciones de cada tipo de triángulo. Por ejemplo, los triángulos agudos son comúnmente utilizados en la arquitectura y diseño, ya que su forma permite una distribución eficiente de fuerzas. Los triángulos rectángulos, por su parte, son fundamentales en la trigonometría y son la base de muchas fórmulas matemáticas, como el teorema de Pitágoras. Finalmente, los triángulos obtusos poseen un aspecto más amplio y son menos comunes en términos de aplicaciones prácticas, pero son igualmente importantes en el estudio de geometría.
Clasificación de triángulos según sus ángulos
- Triángulo Agudo: Todos sus ángulos son menores de 90 grados.
- Triángulo Rectángulo: Tiene un ángulo recto (90 grados).
- Triángulo Obtuso: Uno de sus ángulos es mayor de 90 grados.
Además de la clasificación según los ángulos, los triángulos también se pueden clasificar según sus lados, lo que nos permite tener una visión más completa de esta figura geométrica. En este contexto, la combinación de las clasificaciones por ángulos y por lados proporciona una comprensión más profunda de la geometría de los triángulos y sus propiedades.
Ejemplos prácticos de triángulos según sus ángulos
A continuación, se presentan algunos ejemplos que ilustran cada tipo de triángulo:
- Triángulo Agudo: Un triángulo con ángulos de 50°, 60° y 70°.
- Triángulo Rectángulo: Un triángulo con ángulos de 30°, 60° y 90°.
- Triángulo Obtuso: Un triángulo con ángulos de 120°, 30° y 30°.
Al considerar estas características y ejemplos, se puede apreciar cómo la clasificación de los triángulos según sus ángulos no solo es relevante en el ámbito académico, sino también en aplicaciones prácticas en diversas disciplinas. A lo largo de este artículo, exploraremos en profundidad cada tipo de triángulo, sus propiedades y sus aplicaciones en el mundo real.
Características distintivas de los triángulos según sus lados
Los triángulos se pueden clasificar no solo por sus ángulos, sino también por la longitud de sus lados. Esta segunda clasificación incluye tres tipos principales: equilátero, isósceles y escaleno. Cada uno de estos tipos tiene características únicas que los distinguen.
1. Triángulo Equilátero
Un triángulo equilátero es aquel que tiene los tres lados de igual longitud. Además, todos sus ángulos internos son de 60 grados. Esta simetría lo convierte en una figura muy estéticamente agradable y a menudo se utiliza en arquitectura y diseño.
- Ejemplo: El triángulo de los signos zodiacales es un buen ejemplo de un triángulo equilátero.
- Propiedades:
- Perímetro: Lado × 3
- Área: (Lado² × √3) / 4
2. Triángulo Isósceles
El triángulo isósceles tiene dos lados de igual longitud y un tercer lado que es diferente. Los ángulos opuestos a los lados iguales también son iguales. Este tipo de triángulo se encuentra comúnmente en la naturaleza, como en las montañas.
- Ejemplo: Una montaña puede formar un triángulo isósceles si consideramos la base como uno de sus lados.
- Propiedades:
- Perímetro: 2 × Lado igual + Base
- Área: (Base × Altura) / 2
3. Triángulo Escaleno
En un triángulo escaleno, los tres lados tienen longitudes diferentes y, por ende, todos sus ángulos son diferentes. Este tipo de triángulo es el más común en la vida diaria, ya que se puede encontrar en diversas estructuras y objetos.
- Ejemplo: La forma de un triángulo de señalización en la carretera es un buen ejemplo de un triángulo escaleno.
- Propiedades:
- Perímetro: Lado 1 + Lado 2 + Lado 3
- Área: Se puede calcular usando la fórmula de Herón, que es √(s × (s – a) × (s – b) × (s – c)), donde s es el semiperímetro.
Tabla Comparativa
| Tipo de Triángulo | Lados | Ángulos |
|---|---|---|
| Equilátero | Tres lados iguales | 60 grados cada uno |
| Isósceles | Dos lados iguales | Dos ángulos iguales |
| Escaleno | Tres lados diferentes | Ángulos diferentes |
Comprender estas características puede ayudar en la resolución de problemas de geometría y en la aplicación de los conceptos en situaciones cotidianas.
Preguntas frecuentes
¿Cuáles son los tipos de triángulos según sus ángulos?
Los triángulos se clasifican en tres categorías: acutángulos, rectángulos y obtusángulos.
¿Qué es un triángulo acutángulo?
Un triángulo acutángulo tiene todos sus ángulos menores de 90 grados.
¿Qué caracteriza a un triángulo rectángulo?
Un triángulo rectángulo tiene un ángulo que mide exactamente 90 grados.
¿Qué es un triángulo obtusángulo?
Un triángulo obtusángulo tiene un ángulo mayor a 90 grados.
¿Cuál es la suma de los ángulos en un triángulo?
En cualquier triángulo, la suma de sus ángulos siempre es 180 grados.
Puntos clave sobre los triángulos según sus ángulos
- Triángulo acutángulo: Todos los ángulos < 90°.
- Triángulo rectángulo: Un ángulo = 90°.
- Triángulo obtusángulo: Un ángulo > 90°.
- Suma de ángulos en un triángulo: 180°.
- Ejemplo de uso: Geometría, arquitectura, diseño.
- Importancia en la trigonometría y cálculo de áreas.
¡Dejanos tus comentarios y no olvides revisar otros artículos de nuestra web que también podrían interesarte!