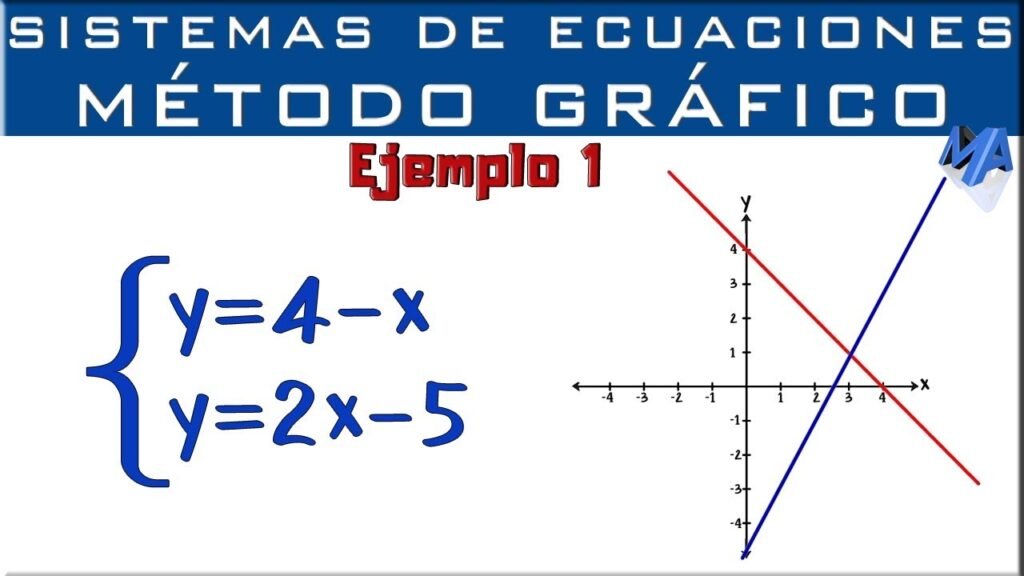
✅ Un sistema de ecuaciones lineales con dos incógnitas es un conjunto de dos ecuaciones que se resuelve usando métodos como sustitución, igualación o eliminación.
Un sistema de ecuaciones lineales con dos incógnitas es un conjunto de dos ecuaciones lineales donde se busca encontrar los valores de dos variables que cumplen ambas ecuaciones simultáneamente. Este tipo de sistemas es fundamental en matemáticas, ya que permite modelar y resolver problemas de la vida real que involucran relaciones lineales entre dos cantidades.
Para resolver un sistema de ecuaciones lineales con dos incógnitas, existen varios métodos, siendo los más comunes el método gráfico, el método de sustitución y el método de eliminación. A continuación, se explicarán cada uno de estos métodos, junto con ejemplos y recomendaciones sobre cuándo utilizarlos.
Método Gráfico
El método gráfico consiste en representar cada ecuación en un plano cartesiano. Cada ecuación se puede graficar como una línea, y el punto donde se intersectan estas líneas representa la solución del sistema. Este método es útil para visualizar la relación entre las dos variables, pero puede ser impreciso si no se hace con herramientas adecuadas.
- Ventajas: Visualización clara de la solución.
- Desventajas: Menos preciso, especialmente con números fraccionarios o decimales.
Método de Sustitución
El método de sustitución consiste en despejar una variable en una de las ecuaciones y sustituirla en la otra. Esto reduce el sistema a una sola ecuación con una incógnita, que se puede resolver fácilmente. Una vez que se encuentra el valor de una variable, se sustituye de nuevo para encontrar la otra.
- Despejar una variable.
- Sustituir en la otra ecuación.
- Resolver la ecuación resultante.
- Encontrar el valor de la primera variable.
Método de Eliminación
El método de eliminación implica sumar o restar las ecuaciones para eliminar una de las variables. Este enfoque es especialmente efectivo cuando las ecuaciones están alineadas de tal manera que se pueden cancelar fácilmente. Al igual que en el método de sustitución, se resolverá una sola variable y luego se sustituirá para encontrar el valor de la otra.
- Ventajas: Puede ser más rápido que el método de sustitución en algunos casos.
- Desventajas: Puede requerir multiplicar las ecuaciones para igualar coeficientes.
Ejemplos y ejercicios prácticos son esenciales para entender cómo aplicar cada método. A medida que practiques, notarás que algunos métodos son más convenientes que otros dependiendo del sistema específico que estés resolviendo.
Métodos gráficos y algebraicos para resolver sistemas de ecuaciones lineales
Los sistemas de ecuaciones lineales pueden resolverse utilizando diversos métodos, cada uno con sus propias características y ventajas. Los dos enfoques más comunes son los métodos gráficos y algebraicos. A continuación, exploraremos ambas técnicas en detalle.
Método gráfico
El método gráfico consiste en representar las ecuaciones lineales en un plano cartesiano y encontrar el punto de intersección de las rectas que las representan. Este método es visual y permite entender la relación entre las ecuaciones de una manera más intuitiva.
- Pasos para resolver un sistema de ecuaciones lineales gráficamente:
- Transformar cada ecuación en la forma y = mx + b, donde m es la pendiente y b es la intersección con el eje Y.
- Graficar cada recta en el plano cartesiano.
- Identificar el punto de intersección, que representa la solución del sistema.
Por ejemplo, si tenemos el siguiente sistema de ecuaciones:
- 1. y = 2x + 1
- 2. y = -x + 4
Al graficar ambas ecuaciones, podemos observar que se intersectan en el punto (1, 3), lo que indica que x = 1 y y = 3 es la solución del sistema.
Métodos algebraicos
Los métodos algebraicos, a diferencia del método gráfico, se enfocan en manipular las ecuaciones para encontrar la solución sin necesidad de graficar. Existen varios métodos algebraicos, entre los más comunes se encuentran:
- Método de sustitución
- Despejar una variable en una de las ecuaciones.
- Sustituir esa expresión en la otra ecuación y resolver.
- Finalmente, utilizar el valor encontrado para obtener el valor de la otra variable.
- Método de igualación
- Despejar la misma variable en ambas ecuaciones.
- Igualar las dos expresiones y resolver.
- Usar el valor obtenido para encontrar la otra variable.
- Método de eliminación
- Multiplicar las ecuaciones si es necesario para que los coeficientes de una de las variables sean opuestos.
- Sumar o restar las ecuaciones para eliminar una variable.
- Resolver la ecuación resultante y luego sustituir para encontrar la otra variable.
Ejemplo práctico utilizando el método de eliminación
Consideremos el sistema:
- 1. 2x + 3y = 12
- 2. 4x – y = 5
Usando el método de eliminación:
- Multiplicamos la segunda ecuación por 3 para igualar los coeficientes de y:
- 12x – 3y = 15
- Sumamos ambas ecuaciones:
- (2x + 3y) + (12x – 3y) = 12 + 15
- 14x = 27 → x = 27/14
- Ahora sustituimos el valor de x en una de las ecuaciones originales para encontrar y.
Este enfoque puede parecer más complicado que el gráfico, pero es muy eficaz para obtener soluciones precisas en menos tiempo, especialmente en casos donde las ecuaciones son más difíciles de graficar.
Tanto los métodos gráficos como los algebraicos son herramientas valiosas para resolver sistemas de ecuaciones lineales. La elección del método dependerá de las preferencias personales y del contexto del problema a resolver.
Preguntas frecuentes
¿Qué es un sistema de ecuaciones lineales?
Es un conjunto de dos o más ecuaciones que comparten las mismas variables y se resuelven simultáneamente para encontrar sus valores.
¿Cómo se representan gráficamente?
Las ecuaciones se grafican como líneas en un plano cartesiano, donde la solución del sistema es el punto de intersección de las líneas.
¿Cuáles son los métodos para resolver un sistema de ecuaciones?
Los métodos más comunes son el método gráfico, el método de sustitución y el método de eliminación.
¿Se puede resolver un sistema de ecuaciones sin solución?
Sí, un sistema puede ser inconsistente, lo que significa que no hay ningún punto que satisfaga todas las ecuaciones simultáneamente.
¿Qué es un sistema compatible?
Es aquel que tiene al menos una solución. Puede ser determinado (una única solución) o indeterminado (infinitas soluciones).
| Punto clave | Descripción |
|---|---|
| Sistema de ecuaciones | Conjunto de ecuaciones lineales que comparten variables. |
| Gráfica | Representación de ecuaciones como líneas en un plano. |
| Método gráfico | Consiste en graficar las ecuaciones y encontrar la intersección. |
| Método de sustitución | Despejar una variable y sustituirla en la otra ecuación. |
| Método de eliminación | Sumar o restar las ecuaciones para eliminar una variable. |
| Sistema inconsistente | No tiene solución; las líneas son paralelas. |
| Sistema compatible | Tiene al menos una solución; puede ser determinado o indeterminado. |
¡Nos encantaría saber tu opinión! Deja tus comentarios y no olvides revisar otros artículos en nuestra web que también podrían interesarte.