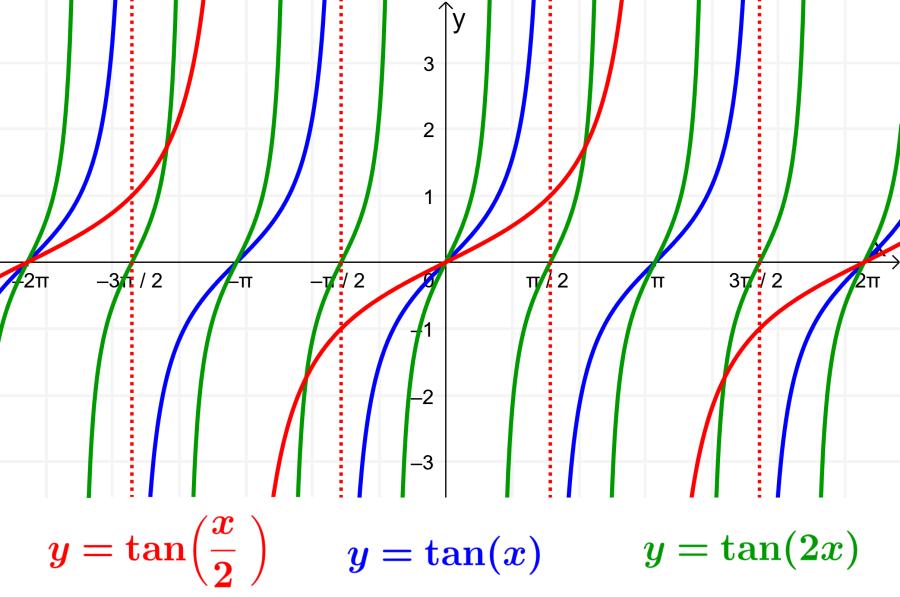
✅ La derivada mide cambios instantáneos; es clave para optimizar recursos, maximizar ganancias, y predecir tendencias en economía, física y más.
La derivada en matemáticas es una herramienta fundamental que permite calcular la tasa de cambio de una función respecto a una de sus variables. En términos simples, nos dice cómo cambia el valor de una función si hacemos pequeñas variaciones en su entrada. Este concepto tiene una amplia gama de aplicaciones, no solo en matemáticas puras, sino también en campos como la física, la economía y la biología, donde se busca entender el comportamiento de sistemas dinámicos.
Las aplicaciones prácticas de las derivadas son numerosas y diversas. Por ejemplo, en la economía, las derivadas se utilizan para determinar la maximización de beneficios o la minimización de costos. En física, son esenciales para estudiar el movimiento de los objetos, ya que nos permiten calcular la velocidad y la aceleración. En biología, se emplean para modelar el crecimiento poblacional y la propagación de enfermedades. A continuación, exploraremos algunos ejemplos concretos y recomendaciones sobre cómo las derivadas impactan nuestra vida cotidiana.
Ejemplos de aplicaciones de las derivadas en la vida real
- Economía: La función de costos y beneficios puede ser analizada mediante derivadas para encontrar puntos óptimos que maximicen las ganancias.
- Física: La derivada de la posición con respecto al tiempo nos da la velocidad, mientras que la derivada de la velocidad con respecto al tiempo nos proporciona la aceleración.
- Biología: Al estudiar el crecimiento de las poblaciones, las derivadas se utilizan para modelar las tasas de reproducción y mortalidad, ayudando a predecir cambios demográficos.
Consejos para entender y aplicar derivadas
Para aquellos que deseen profundizar en el uso de las derivadas, aquí hay algunas recomendaciones:
- Practica con ejemplos: La mejor manera de entender las derivadas es a través de ejercicios prácticos que conecten el concepto con situaciones reales.
- Utiliza software de matemáticas: Herramientas como GeoGebra o Mathematica permiten visualizar cómo cambian las funciones y sus derivadas.
- Estudia el contexto: Relaciona las derivadas con temas de tu interés, como la economía o la biología, para hacer el aprendizaje más relevante.
Las derivadas no son solo un concepto abstracto dentro del campo de las matemáticas, sino que tienen un impacto significativo en nuestra comprensión del mundo. Desde la optimización de recursos hasta el análisis de fenómenos naturales, su aplicación es vital en diversos ámbitos. En el siguiente apartado, profundizaremos en el cálculo de derivadas y sus propiedades más relevantes.
Ejemplos prácticos de derivadas en problemas cotidianos
Las derivadas no solo son un concepto teórico en el ámbito de las matemáticas, sino que también tienen aplicaciones muy reales en nuestra vida diaria. A continuación, exploraremos algunos ejemplos prácticos que nos ayudarán a entender mejor su relevancia.
1. Cálculo de velocidad
Una de las aplicaciones más comunes de la derivada es en el cálculo de la velocidad. Por ejemplo, si un automóvil viaja a lo largo de una carretera y su posición está dada por la función s(t), donde t es el tiempo, la velocidad del automóvil en un instante dado se puede calcular como la derivada de s respecto a t:
v(t) = s'(t)
Si la posición de un auto se describe por la función s(t) = 5t^2, la derivada sería:
s'(t) = 10t
Esto significa que a los 2 segundos, la velocidad del auto sería:
v(2) = 10 * 2 = 20 m/s
2. Optimización de costos
En el mundo empresarial, las derivadas se utilizan para optimizar costos y maximizar beneficios. Por ejemplo, si una empresa tiene una función de costo C(x) que depende de la cantidad de productos x que produce, al derivar C respecto a x se puede determinar el costo marginal:
C'(x) = C(x + 1) – C(x)
Esto permite a la empresa decidir si vale la pena producir una unidad adicional. Si C'(x) es negativo, significa que el costo disminuirá si se produce más.
3. Tasa de cambio en población
Las derivadas también se utilizan para modelar el crecimiento de la población. Supongamos que la población de una ciudad está modelada por la función P(t). La tasa de cambio de la población en el tiempo se puede calcular como:
P'(t) = dP/dt
Si se estima que la población crece según la fórmula P(t) = 1000e^{0.03t}, la tasa de crecimiento en un determinado tiempo t se puede obtener al derivar la función:
P'(t) = 30e^{0.03t}
Esto proporciona una herramienta valiosa para los planificadores urbanos y autoridades gubernamentales al tomar decisiones sobre infraestructura y servicios públicos.
4. Aplicaciones en la física
En física, el concepto de aceleración se calcula utilizando derivadas. La aceleración es, de hecho, la derivada de la velocidad respecto al tiempo:
a(t) = v'(t)
Si la velocidad de un objeto es dada por la función v(t) = 3t^2 + 2t, al derivar se obtiene:
a(t) = 6t + 2
Esto permite a los físicos predecir cómo cambiará la velocidad de un objeto en movimiento, lo cual es fundamental en el estudio de la dynamics.
5. Uso en finanzas
En el ámbito financiero, las derivadas son útiles para analizar el comportamiento de los mercados. Por ejemplo, si una función f(x) representa el valor de una acción en función del tiempo, la derivada f'(x) indica si el valor de la acción está aumentando o disminuyendo:
- Si f'(x) > 0: la acción está en alza.
- Si f'(x) < 0: la acción está en baja.
Los inversionistas utilizan esta información para tomar decisiones informadas sobre la compra y venta de acciones.
Tabla resumen de aplicaciones
| Aplicación | Función | Derivada | Interpretación |
|---|---|---|---|
| Velocidad | s(t) = 5t² | s'(t) = 10t | Velocidad instantánea |
| Costo | C(x) | C'(x) | Costo marginal |
| Población | P(t) = 1000e^{0.03t} | P'(t) = 30e^{0.03t} | Tasa de crecimiento poblacional |
| Aceleración | v(t) = 3t² + 2t | a(t) = 6t + 2 | Cambio en la velocidad |
| Finanzas | f(x) | f'(x) | Comportamiento del mercado |
Como hemos visto, las derivadas son herramientas poderosas que nos permiten entender y resolver problemas en diversas áreas de nuestra vida cotidiana. Desde la velocidad de un automóvil hasta el crecimiento poblacional, su aplicación es rica y variada.
Preguntas frecuentes
¿Qué es una derivada?
Una derivada es una medida de cómo una función cambia a medida que su variable independiente cambia. Representa la pendiente de la tangente en un punto específico de la curva.
¿Para qué se utilizan las derivadas?
Se utilizan en diversas áreas como la física para calcular velocidad y aceleración, en economía para maximizar beneficios o minimizar costos, y en biología para modelar el crecimiento poblacional.
¿Cómo se aplica la derivada en la vida real?
En la vida cotidiana, se emplean derivadas para optimizar procesos, como encontrar el punto más eficiente para producir bienes o minimizar tiempos de entrega en logística.
¿Qué es la regla de la cadena?
La regla de la cadena es un método para calcular la derivada de funciones compuestas. Es fundamental para simplificar el proceso de derivación cuando las funciones están encadenadas.
¿Qué aplicaciones tiene en la ingeniería?
En ingeniería, las derivadas son esenciales para el análisis de estructuras, diseño de sistemas de control y optimización de recursos en proyectos de construcción.
¿Cómo se relacionan las derivadas y las integrales?
Las derivadas y las integrales son conceptos fundamentales del cálculo, siendo la integral una operación inversa a la derivada. Juntas forman el teorema fundamental del cálculo.
| Punto clave | Descripción |
|---|---|
| Definición | La derivada mide la tasa de cambio de una función. |
| Uso en Física | Calcula velocidad y aceleración. |
| Uso en Economía | Maximiza beneficios y minimiza costos. |
| Optimización | Ayuda a encontrar soluciones óptimas en diferentes contextos. |
| Ingeniería | Analiza estructuras y sistemas complejos. |
| Teorema Fundamental | Relación entre derivadas e integrales. |
¡Nos encantaría conocer tu opinión! Deja tus comentarios y no olvides revisar otros artículos en nuestra web que también pueden interesarte.