✅ Para calcular el área de un triángulo: (base x altura) / 2. Para el perímetro: suma de todos los lados. ¡Matemáticas simplificadas!
Calcular el área y el perímetro de un triángulo es un proceso sencillo que puede realizarse con fórmulas básicas. Para el área, se utiliza la fórmula A = (base × altura) / 2, donde la base y la altura son medidas del triángulo. En cuanto al perímetro, se suma la longitud de los tres lados: P = lado1 + lado2 + lado3. Conociendo estas fórmulas, cualquier persona puede calcular rápidamente estas medidas.
Te enseñaremos no solo cómo aplicar estas fórmulas, sino también cómo hacerlo con diferentes tipos de triángulos, como el triángulo equilátero, el triángulo isósceles y el triángulo escaleno. Además, proporcionaremos ejemplos prácticos y consejos útiles para facilitar el entendimiento del tema.
Fórmulas básicas para el cálculo
Las dos fórmulas fundamentales para calcular el área y el perímetro de un triángulo son:
- Área: A = (base × altura) / 2
- Perímetro: P = lado1 + lado2 + lado3
Cálculo del área
Para calcular el área de un triángulo, necesitas conocer la base y la altura. Por ejemplo, si la base mide 5 cm y la altura 4 cm, el cálculo sería:
A = (5 cm × 4 cm) / 2 = 10 cm²
Cálculo del perímetro
El perímetro de un triángulo se obtiene sumando las longitudes de sus lados. Si los lados miden 5 cm, 6 cm y 7 cm, el cálculo sería:
P = 5 cm + 6 cm + 7 cm = 18 cm
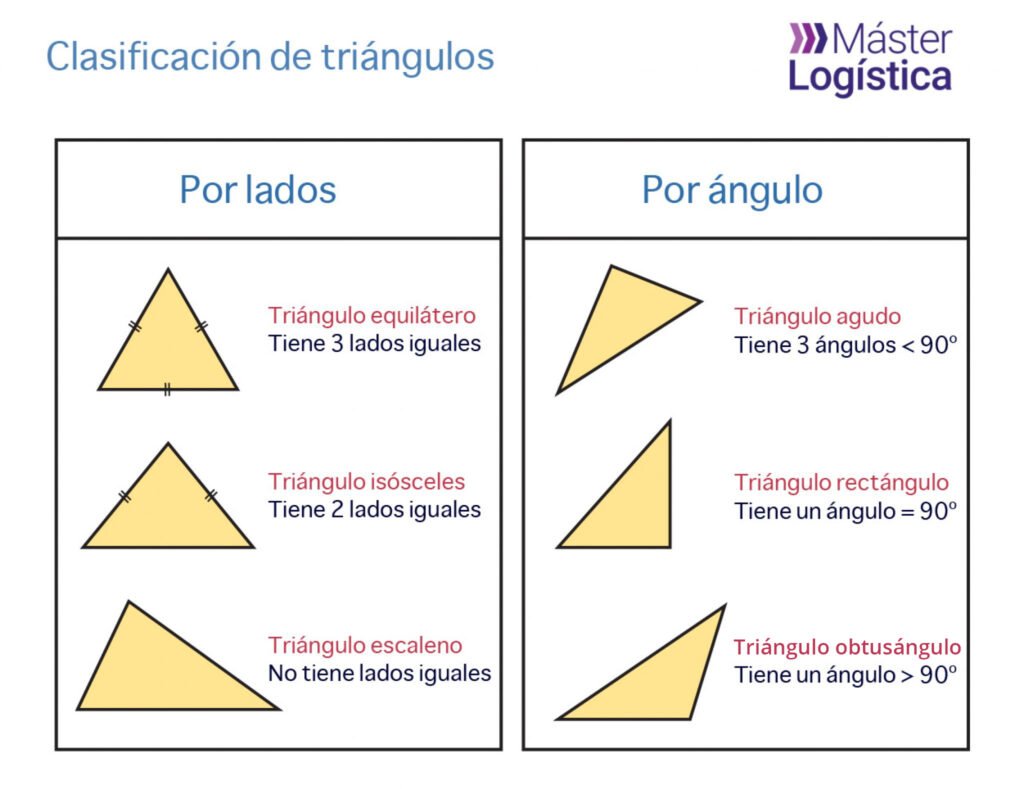
Tipos de triángulos y sus características
Existen diferentes tipos de triángulos, cada uno con sus propias características y formas de calcular el área y el perímetro:
- Triángulo equilátero: Todos los lados son iguales. Si el lado mide ‘a’, el área se calcula como A = (√3/4) × a².
- Triángulo isósceles: Dos lados son iguales. Si la base mide ‘b’ y los otros lados ‘a’, el área se puede calcular como A = (b × altura) / 2.
- Triángulo escaleno: Todos los lados son diferentes. Se puede usar la fórmula de Herón para el área: A = √(s(s-a)(s-b)(s-c)), donde ‘s’ es el semiperímetro y se calcula como s = (a+b+c)/2.
Consejos para facilitar el cálculo
Aquí hay algunos consejos para ayudarte a calcular el área y el perímetro de un triángulo de manera más efectiva:
- Siempre mide en las mismas unidades (cm, m, etc.) para evitar errores.
- Utiliza una calculadora para evitar errores en los cálculos manuales.
- Si es posible, dibuja el triángulo y anota las medidas para tener una referencia visual.
Ejemplos prácticos para aplicar fórmulas de área y perímetro
Calcular el área y el perímetro de un triángulo puede parecer complicado al principio, pero con algunos ejemplos prácticos, se vuelve mucho más sencillo. A continuación, veremos varios casos que ilustran cómo aplicar las fórmulas de forma efectiva.
Ejemplo 1: Triángulo Equilátero
Un triángulo equilátero tiene todos sus lados de igual longitud. Supongamos que cada lado mide 6 cm.
- Perímetro: Para calcular el perímetro, utilizamos la fórmula P = 3 × L, donde L es la longitud de un lado.
- P = 3 × 6 cm = 18 cm
Para calcular el área, utilizamos la fórmula A = (√3 / 4) × L².
- A = (√3 / 4) × 6²
- A = (√3 / 4) × 36 = 9√3 cm² ≈ 15.59 cm²
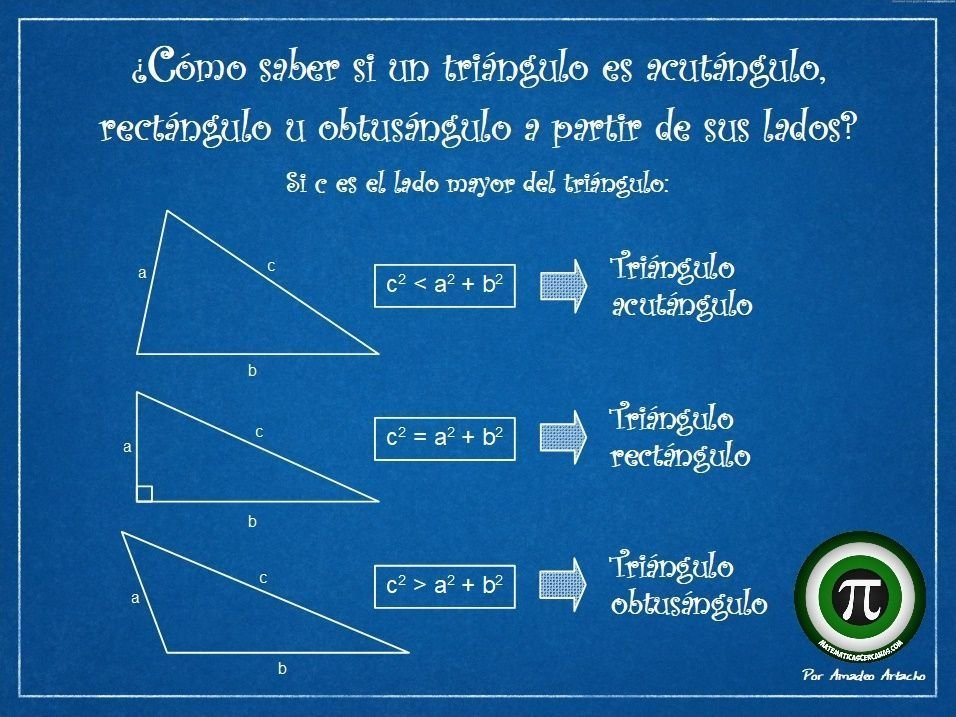
Ejemplo 2: Triángulo Rectángulo
Consideremos un triángulo rectángulo donde uno de los catetos mide 3 cm y el otro 4 cm.
- Para calcular el área, usamos la fórmula A = (base × altura) / 2.
- A = (3 cm × 4 cm) / 2 = 6 cm²
El perímetro se calcula sumando las longitudes de los tres lados. Primero, debemos encontrar la hipotenusa usando el teorema de Pitágoras:
- C² = A² + B²
- C² = 3² + 4² = 9 + 16 = 25
- C = √25 = 5 cm
Por lo tanto, el perímetro es:
- P = 3 cm + 4 cm + 5 cm = 12 cm
Ejemplo 3: Triángulo Escaleno
Ahora, consideremos un triángulo escaleno donde los lados miden 5 cm, 7 cm y 8 cm. Para calcular el perímetro, simplemente sumamos los lados:
- P = 5 cm + 7 cm + 8 cm = 20 cm
Para calcular el área, podemos utilizar la fórmula de Herón. Primero, calculamos el semiperímetro s:
- s = P / 2 = 20 cm / 2 = 10 cm
Luego, aplicamos la fórmula:
- A = √(s × (s – a) × (s – b) × (s – c))
- A = √(10 cm × (10 cm – 5 cm) × (10 cm – 7 cm) × (10 cm – 8 cm))
- A = √(10 × 5 × 3 × 2) = √300 ≈ 17.32 cm²
Estos ejemplos prácticos demuestran cómo aplicar las fórmulas de área y perímetro en diferentes tipos de triángulos. Recuerda que practicar con distintas medidas te ayudará a familiarizarte con los cálculos. ¡No dudes en experimentar con diferentes longitudes y formas!
Preguntas frecuentes
¿Cómo se calcula el área de un triángulo?
El área se calcula con la fórmula: Área = (base * altura) / 2.
¿Qué es el perímetro de un triángulo?
El perímetro es la suma de las longitudes de todos sus lados: Perímetro = lado1 + lado2 + lado3.
¿Qué información necesito para calcular el área?
Necesitas conocer la base y la altura del triángulo.
¿Puedo calcular el área si solo tengo los tres lados?
Sí, puedes usar la fórmula de Herón: Área = √(s * (s – a) * (s – b) * (s – c)), donde s es el semiperímetro.
¿Qué tipos de triángulos existen?
Existen triángulos equiláteros, isósceles y escalenos, según las longitudes de sus lados.
¿Cómo se relacionan el área y el perímetro en un triángulo?
El área mide la superficie, mientras que el perímetro mide la longitud total de sus lados; son conceptos diferentes.
Puntos clave sobre el área y el perímetro del triángulo
- Área = (base * altura) / 2
- Perímetro = lado1 + lado2 + lado3
- Fórmula de Herón para área con lados conocidos: Área = √(s * (s – a) * (s – b) * (s – c))
- Semiperímetro: s = (lado1 + lado2 + lado3) / 2
- Triángulos equiláteros tienen todos sus lados y ángulos iguales.
- Triángulos isósceles tienen dos lados iguales.
- Triángulos escalenos no tienen lados ni ángulos iguales.
- La altura se traza desde un vértice hasta la base perpendicularmente.
¡Dejanos tus comentarios y no olvides revisar otros artículos de nuestra web que también pueden interesarte!